Monthly Archives: May 2020

05/18/20

Comments on J.B. Stump’s Article (2020) “Did God Guide Our Evolution?”

0001 These comments are offered on my blog as a sample of the character of works that are available for sale at www.smashwords.com.  They seem rather dry and technical.  Nevertheless, they offer an innovative postmodern approach that should interest enterprising students and scholars.  Here, the category-based nested form and the two-level interscope come into play.

These categorical structures are introduced in A Primer on the Category-Based Nested Form and A Primer on Sensible and Social Construction.

0002 J.B. Stump offers his views in the March issue of Perspectives on Science and Christian Faith (volume 72(1), pages 15-24).  Perspectives is the flagship publication of the American Scientific Affiliation.  Stump’s article may be available for download at their website.  If not, please request.

Stump addresses the question, “Did God guide our evolution?”

He reviews several broad ways to answer, then discusses his favorite.

0003 So, does God guide our creation?

What about the scientific description of human evolution?

These questions point in different directions, C2 and C1.

The second direction (C2) is that God intentionally creates human beings in His image.

The first direction (C1) claims that evolution is the best scientific explanation for the origin of our species, Homo sapiens.

0004 These two claims can both be formulated as category-based nested forms (CBNF).

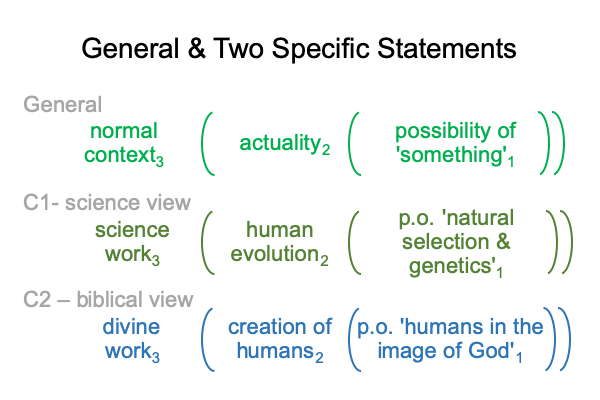
The CBNF contains four expressions.  The fourth is paradigmatic.  A normal context3 brings an actuality2 into relation with the possibility of ‘something’1.  The subscripts refer to Peirce’s categories.

0005 Now, I associate features in each direction to the CBNF.

The normal context3 for C1 is science3.  The normal context3 for C2 is the Genesis portrayal of God’s work3.

The actuality2 for C1 is human evolution2 and for C2 is the Genesis creation of humans2.

The potential1 for C1 is ‘natural selection and genetics’1.  The potential1 for C2 is ‘the picture of humans as images of God’1.

0006 Here is how that looks in technical notation.

0007 So, did God guide our evolution?

According to Stump, the first strategy (A1) for answering the question relies on semantics.

I ask, “What problem does semantics solve?”

Well, I see two nested forms.  How do they interact?

0008 Normal contexts follow the logic of exclusion, alignment and complement.

If they exhibit the logic of exclusion, the nested forms come into conflict.  It’s God’s work3 or science work3.  It is either one or the other.

If the logic is complement, then one could end up with Steven Gould’s idea of “non-overlapping magisteria”.  This is not much of a complement.  Perhaps, a truce is a better description.

If they exhibit the logic of alignment, then one nested form virtually emerges from (and situates) the other.  This structural relation is called a “two-level interscope”.  The two levels are contenta and situationb.  Contenta goes with Peirce’s category of firstness (the realm of possibility).  Situationb associates with Peirce’s category of secondness (the realm of actuality).

The two-level interscope has two flows.

In the upward flow, contenta underlies situationb.

In the downward flow, situationb orders contenta.

0009 So, I have two statements (C2 and C1) and two levels.  Which goes with which?

Here is where semantics comes into play.  Semantics is about language.  When I talk about science, my words are usually content-oriented.  When I think about God’s creation, I am contemplating my own (and everyone else’s) situation.

There is another, more technical semantic argument.  The religious statement (C2) cannot be situated by the science statement (C1), because the Positivist’s judgment rules out metaphysics.  The Positivist’s judgment is developed in Comments on Jacques Maritain’s Book (1935) Natural Philosophy.  I cannot help but smile at this application.  From a semantic point of view, how could science situate a nested form that it cannot consider?

Here is a picture of the semantic-ordered, two-level interscope.

Figure 2

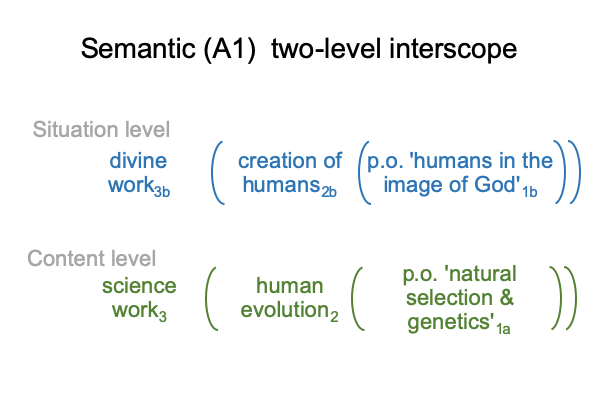
0010 Ironically, this model initiates questions that key into Stump’s second answer, the nomological strategy (A2).  The nomological strategy suggests that the laws of human evolution are not well understood.  The laws of evolution may be, but there is something wrong with their application to human evolution.  Stumps reviews some critical arguments.

0011 The two-level interscope pictured above endorses the “yes, but” character of the nomological approach, addressing the question, “Did God guide human evolution?”

If science is so smart, then it should situate the religious nested form, rather than the other way around.  The fact that the Positivist judgment excludes metaphysics indicates that science can understand human evolution only in terms of material and instrumental causalities.  However, I personally situate the evolution of my species in terms of my religious sensibility, which involves immaterial causalities, such as final attributes and formal design.

What does this imply?

The ultimate human niche is not material.

Indeed, this is the central thesis of the masterwork, The Human Niche, available at www.smashwords.com.

0012 The semantic (A1) strategy may be adjusted by the nomological (A2), producing something like this.

Figure 3

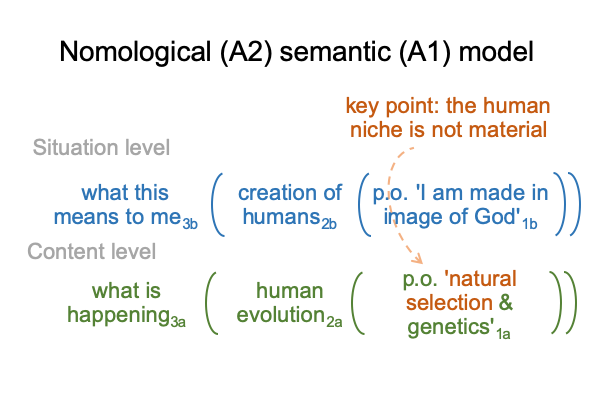
0013 Well, if our hominin ancestors adapted over millions of years into a niche that is not material, then the third answer, the causal joint strategy (A3), comes into play.  The causal joint strategy suggests that God does not obviously intervene in human evolution, but God nevertheless creates.  The question is, “How?”  Stump considers several authors with very curious answers.

0014 These answers have something in common.

They exploit the dynamics of the two-level interscope.

The divine situationb guides the science contenta.

The scientific contenta underlies divine subtle interventionb.

“Subtle” means “below the threshold of detection”.

0015 How could this happen?

I only need to substitute God’s Will3b for the situation-level actuality3b and God’s Presence1b for the situation-level potential1b.

Here is how that looks.

Figure 4

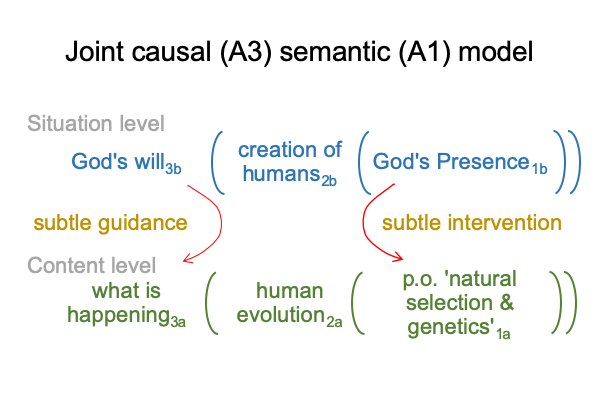
0016 God’s Will3b associates to God’s work3b and what this means to me3b.

God’s Will3b provides subtle guidance to science work3a and what is happening3a.

Subtle guidance underlies the Anthropic Principle.

God’s Presence1b associates to the potential of humans (including me) being created in the image of God1b.

0017 How does God’s Presence1b manifest?

God’s Presence1b is the potential underlying God’s will3b.  Also, it1b stands in the slot 1b, which is the potential1b of situating the content level actuality2a.  This associates God’s Presence1b with the potential of situating human evolution2a.

This potential to situate operates according to joint causes, in the realm of possibility1.

God’s Presence1b virtually situates (and is emergent to) the potential of ‘natural selection and genetics’1b.  The word, “virtual”, means “in virtue” (rather than the modern use, “in simulation”).  The term, “in virtue”, goes with final attributes and formal design.

So, while the stuff of Neodarwinism may be scientifically regarded according to material and instrumental causes, the virtue of God’s Presence1b cannot be fully ignored in either the adaptation1a or the phenotype1a.  This is the central point of the joint causal (A3) answer.  Biologists cannot avoid joint causality when they discuss adaptation or phenotype.  Many modern biologists label God’s Presence1b, “chance1b” or “random1b”.

0018 In sum, divine subtle intervention operates in the realms of normal context3 and potential1, as pictured above.  Neither of these can be scientifically observed or measured.

0019 The pertinence of the joint causal (A3) semantic (A1) approach does not stop there.

Adaptations1a and phenotypes1a are actualities that have the potential1a of underlying human evolution2a.

That means that adaptations2 and phenotypes2 are actualities with their own nested forms.

One can imagine that God directly intervenes in either nested form by manipulating its underlying potential.  Such intervention avoids detection because the actualities, adaptation2 and phenotype2 refer to the same biological entity2.  In other words, two actualities2 constitute a single entity2.  Therefore, the two actualities2 are confounded.

0020 Let me develop this scenario in a little more detail.

Neodarwinism1a consists in two independent nested forms, as noted in Comments on Dennis Venema and Scot McKnight’s Book (2017) Adam and the Genome.  These nested forms belong to the situation-level of a two-level interscope.

In one, natural selection3b brings adaptation2b into relation with a niche1b.  The niche1b is the potential1b of situating an actuality independent of the adapting species2a.

In the other, body development3b brings phenotype2b into relation with genotype1b.  The genotype1b is the potential1b of situating DNA2a.

In the joint causal answer, God could directly manipulate either an actuality independent of the adapting species2a, the foundation of the niche1b, or DNA2a, the foundation of the genotype1b, without detection.  Why?  A change in one can mask a change in the other.  They are confounders.

0021 Here is a picture of these independent category-based nested forms.

Figure 5

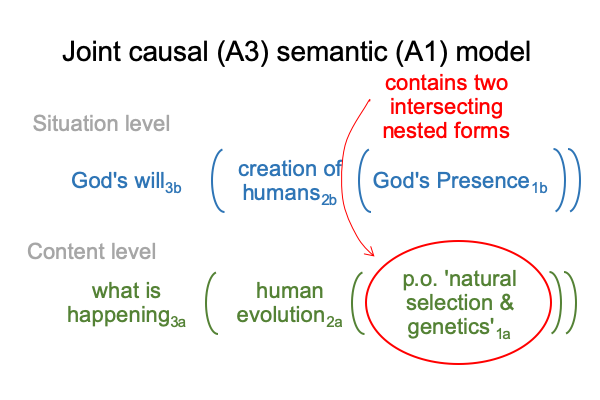
0022 The adaptation2 is not the same as the phenotype2.  Each arises from a different potential1.  Each requires its own normal context3.  However, adaptation2 and phenotype2 pertain to a single actuality2, the biological entity, in this case, the human being2.  The human being is the intersection of adaptation2 and phenotype2.

According to the chapter on presence in How to Define the Word “Religion”, intersections are mysterious.  They contain contrasting features that cannot be resolved through the logic of noncontradiction.  Biologists present distorted views when they claim that evolution consists in either natural selection or DNA-based body development.  The intersection of these two nested forms codifies what biologists are really trying to say, but fail, because of preferences for either natural history or genetics.

0023 So, the joint causal answer suggests that, even if God directly manipulates the actualities underlying the niche1b or the genotype1b, scientists could never detect the intervention, because the evolved biological entity2 is an intersection, filled with contradictions.

Here is how that looks.

Figure 6

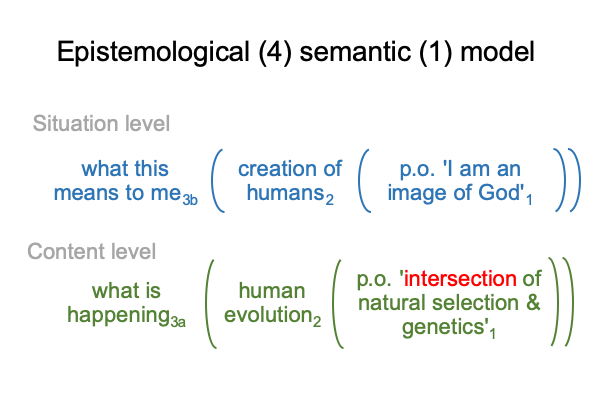
0024 This brings me to Stump’s favorite strategy (A4), the epistemological.

The epistemological strategy highlights the contrast between science work3a and God’s work3b, while simultaneously asserting that they cannot be divorced.  I am a product of human evolution2a.  I am created in the image of God2b.  Science work3a is what is happening3a. God’s work3b is what this means to me3b.

Here is a picture of that strategy.

Figure 7

0025 Now, I address the elephant in Stump’s room.

I do so in a roundabout way.

I start with a question about the question.

0026 Does God guide human evolution?

What is the difference between this question and…

Did God guide human evolution?

0026 One strategy to answer this question is semantic (A1).

Human evolution is in our past.  Are we no longer are evolving?  It sure seems that we aren’t.  In fact, who knows what we are doing?

0027 What does this imply?

The nomological strategy (A2) comes to bat. 

Homo sapiens comes into existence, and lives for some time, in the Lebenswelt that we evolved in.

Currently, we are no longer in the Lebenswelt that we evolved in.

Therefore, our current Lebenswelt is not the Lebenswelt that we evolved in.

I conclude that a transition from one Lebenswelt to the other is missing in current accounts of human evolution.

This missing element is hypothesized in The First Singularity and Its Fairy Tale Trace and reflected upon in Comments on Original Sin and Original Death: Romans 5:12-19.  This transition is dramatized in An Archaeology of the Fall, available on www.smashwords.com.

0028 With this said, the joint causal strategy (A3) cannot be ignored.

If (as proposed in The Human Niche), humans adapt into the niche of immaterial triadic relations (such as the category-based nested form), then God’s work3b virtually situates nature’s operations, as understood by science3a.  In our evolution, the material world enters into an evolving awareness of immaterial triadic relations, without compromising its instrumental and material causalities.

0029 On top of that, the epistemological strategy (A4) says that God’s work3b and science work3a cannot be divorced, in the same way that what this means to me3b cannot be divorced from what is happening3a.

0030 So obviously, the elephant in the room is concordism.

Did God guide human evolution?  How does God guide us today?

These questions aim to harmonize scientific formulations and Biblical revelation.

Stump is on target.  Four different strategies apply.  But, the target is so much larger than he realizes.

For example, Comments on Christy Hemphill’s Essay (2019) “All in a Week’s Work” introduces a harmony between cognitive psychology and metaphors within Genesis 1.

The concord between humans created in the image of God2b and human evolution2a will prove to be multi-faceted, addressing who we are2b as well as who we evolved to be2a.

0031 My thanks to J.B. Stump for publishing his evocative article.

****

Feel free to e-mail comments and corrections.

05/6/20

A Theology of the Deep State (Part 1)

It is official.  The federal government has established a religion.  May I propose a label for this new referent?  Let me call it the “deep state”.

Others call it the “administrative state”.

The imprimatur comes when Steve Deace, broadcasting on Blaze TV from the heart of America’s flyover country, states the obvious, saying, “We are not dealing with a political party.  We are dealing with a cult.”

For example, only a cult can perform the purgation and humiliation rites afforded to Brett Kavanaugh, then a nominee for the Supreme Court of the United States.  Now a member of the SCOTUS, this individual is forever branded by one accusation.  The accusation, while never proven true, is justified by its reliance on an organizational objective, claiming, “Believe the woman, for … (whatever righteousness applies)”.

Righteousness1aC is the nectar of religion.

Organizational objectives2aC are like gods.

Hey, what are those subscripts?

Subscripts are introduced in A Primer on the Category-Based Nested Form and A Primer on Sensible and Social Construction.  The “1” indicates Peirce’s category of firstness, the realm of possibility.  The “2” denotes actuality in a category-based nested form.  The “a” refers to the content-level of an interscope (a category-based nested form composed of category-based nested forms).  The “C” points to the society tier (the third tier in a category-based nested form composed of interscopes).

The three tiers are societyC, organizationB and individual in communityA.

Yes, this notation introduces a novel approach to Sociology.

Plus, this approach is worth looking into.  Homeschoolers should consider the course titled, How to Define the Word “Religion”.

Why?

State indoctrinators define the word so narrowly that it seems that they are covering up a topic much larger, and more interesting, than churches, synagogues and mosques.

This brings me back to the prescience of the broadcaster noted above.

The immediate stimulus for the broadcaster’s response is a coronavirus-related national work-stoppage.  The statistics associated with the unfolding pandemic simply do not support the drastic, uni-dimensional, solution of a total shutdown, bringing the US economy to a standstill.

Yes, in economics and politics, there are two dimensions.  There are trade-offs.  

Yet, in the matrix of the administrative state, there are only organizational objectives2aC.  The Center for Disease Control (CDC) and other state-cults3aC focus on saving lives2aC.  We must save lives at all costs1aC.

Organizational objectives2aC emerge from (and situate) the potential of righteousness1aC.

The problem?

They2aC may come into conflict.

One solution endows each insitution3aC with a similar character.  In the case of the deep state, that character is a demand for sovereign power3bC.  Sovereign laws and decrees2bC are necessary in order for each institution3aC to achieve its organizational objectives2aC.  This imperative1cC satisfies the potential underlying all legislation2bC: the possibilities inherent in order1bC.

Picture piglets struggling to latch onto their mother’s teats.  Each has its own agenda.  Of course, these agendas conflict.  Yet, a certain order is achieved as long as the mother offers her milk.

Or consider the abandoned infants, Romulus and Remus, suckling the teats of a she-wolf. Surely, the Romans offer a more evocative icon of the feminine nature of sovereign power.  Believe the she-wolf and she will offer her milk, instead of her teeth.

To Marxists, there is nothing more.  The sovereign3bC must be the exception1cC.  The state3bC must not be subject to its own laws2bC. The milk2cC must flow1cC.  The milk2cC sustains order1cC.  Order1bC is to sovereign power3bC as righteousness3aC is to institutions1aC.  Listen to the speakers.  Hear the talking heads.  Every shill3aC signals a virtue1aCthat calls the citizen to a righteousness1aC that seeks to establish order1bC.

There is nothing above sovereign power3bC.

Yet, there3cC is.

The problem is that we cannot envision it2cC.

Here is a way to picture the society tier for Big Government (il)liberalism.

Figure 1
05/5/20

A Theology of the Deep State (Part 2)

The two-level interscope is typical for sensible construction.  Sensible construction does not ask, “Why?”.  Sensible construction assumes that, whatever we are doing, it’s okay.  The perspective level is never questioned, unless something goes horribly wrong.

Here is a picture of the society tier for Big Government (il)liberalism.

Figure 2

If there is anything hidden within the perspective level, it is this: The milk2bC must flow1cC.

That is, the milk of the federal government2bC.

There are no suggestions for why the milk must flow, except for the fact that so many institutions3aC demand sovereign power3bC in order to implement2bC their organizational objectives2aC.  Institutions3aC that do not appeal to Caesar3bCoften wither or mutate into institutions that do.  Mutation is facilitated through infiltration by believers2cA in a particular (sovereign-entangling) righteousness1aC.

Each organizational objective2aC is a god.

Some call them “sacred cows”.

Since each organizational objective2aC emerges from (and situates) the potential of righteousness1aC and since righteousness1aC is inherently metaphysical in nature, the deep state consists in a wide range of cults (institutions3aC) that have a common feature.  Each righteousness1aC accommodates a call for sovereign power3bC.

Diversity is the strength of Big Government (il)liberalism.

However, there is a problem.

All the advocates claim to be “not religious”, even though they are.

Why?

Why do the advocates for Big Government (il)liberalism, who congregate in cults3aC, claim to be “not religious”?

Well, the American Constitution’s first amendment states that the federal government shall not establish a religion.

Consequently, acolytes of the deep state define “religion” narrowly, with intellectual constriction, as falling into bins labeled “Christian”, “Jewish”, “Islamic” and so forth.  In this way, they skirt the question that cannot be confronted.  Why is their righteousness not “religious” as well?  These state-entangled institutions3aC implement organizational objectives2aC that situate the potential of righteousness1aC.  Why is their metaphysical righteousness exempt?  Why are not they “religious”?

This crucial point is ignored by current experts in Sociology, because they are committed to Big Government (il)liberalism.  Okay, that’s a cheap shot.  But really, the answer demands a definition of the word, “religion”, that does not simply slap labels onto people.  Do any sociological theories explain why the labels work?  Or, do the labels explain themselves?

The course, How to Define the Word “Religion” offers a novel definition, one that is not hemmed in by a deep-state historical narratives or restrictive legalisms.

But wait, the indoctrinated… er, educated citizen replies, “Okay, let’s be sensible.  These state-entangled institutions, and their advocates, say that they are not religious because they are not ‘Christian’, ‘Jewish’, ‘Islamic’ and so forth.  This is obvious.  Everyone agrees.”

Shall I venture a translation?

If you disagree, no milk for you.  Instead, you will feel the sovereign’s teeth.

This is a word-game, where so-called “enlightenment” institutions3aC advocate for certain laws and decrees2bC in order to promulgate their organizational objectives2aC, yet declare themselves to be “not religious”.  Why is their righteousness1aC different from the righteousness1aC of institutions that fall under the label?  How do their missions2aC differ from the Christian, Jewish and Muslim missions2aC?  Why do they say that they are not religious?

Oh, yes, that gets around the first amendment.

Clearly, the veiled perspective levelc of the deep state encourages subsidies2bC for innumerable “points of light”, institutions3aC that self-identify as “not religious”, yet are founded on diverse calls to righteousness1aC.  These cults3aC that have a character in common.  Each point of light3aC signals its virtue1aC, while demanding that state laws and decrees3bC implement its organizational objectives2aC.

The advocate-lobbyist says, “Our missions2aC are ‘not religious’, yet are necessary for the organization of a righteous society.”

The advocate-lobbyist cannot say, “There may be a reason why the organizational objectives2aC of all deep-state institutions3aC call for the exercise of sovereign power3aC. But, we cannot know the reason until the milk becomes all there is.”

Only then, will the veil be pulled back and the perspective levelc revealed.

What do we know?

Big Government (il)liberalism establishes institutions3aC that declare themselves to be “not religious”, even though, like Christian, Jewish and Islamic institutions3aC, they contextualize organizational objectives2aC that emerge from (and situate) the potential of righteousness1aC.  Their declaration exempts them from the first amendment of the American Constitution.

Big Government (il)liberal organizational objectives2aC have a common feature.  Their2aC implementation relies on sovereign power3bC.  Since sovereign power3bC is not subject to its own laws and decrees2bC, then the resulting institutions3aC participate in the sovereign’s state of exception.  In fact, the sovereign3bC is the only one who can bring contemporary trends to fulfillment by cultivating a state of exception2cC.

The federal government not only has established a host of religions3aC, each standing as a point of light in a New World Order, but all these religions3aC vicariously participate in the exception2cC that contextualizes sovereign power3aC.

What does this imply?

The theology of the deep statec is yet to enter into consciousness in our current, Enlightenment-celebrating, Zeitgeist.  State-entangled institutions3aC are everywhere.  Few have eyes to see.  Many avert their gazes.  The suprasovereign levelcC stands behind a curtain and will step out only when a state of exception2cC brings all into relation1cC.  That moment will be a revelation.

There are signs of a future unveiling. The hour draws near.

Consider Comments on Peter Burfiend’s Book (2014) Gnostic America.

Consider Comments on Eric Santner’s Book (2016) The Weight of All Flesh.

These works belong to the Intimations of Political Philosophy series, available at smashwords.

Broadcaster Steve Deace reads the writing on the wall, announcing, “We are not dealing with a political party.  We are dealing with a cult.”

The federal government has established a legion of religions3aC, each declaring itself to be “not religious”.  Plus, each has one other feature in common with all others.    Where are the intellectual tools to articulate these sociological phenomena?